Дзета-функция Римана — это одна из самых важных и знаменитых функций в математике, играющая ключевую роль в теории чисел. Она связана с распределением простых чисел и имеет широкие применения в различных областях науки и техники, включая криптографию, математическую физику и аналитическую теорию чисел. Эта функция, несмотря на свою кажущуюся простоту, открывает перед исследователями целый мир математических загадок и гипотез, одна из которых — гипотеза Римана — остаётся одной из самых сложных и нерешённых проблем в математике.
В этой статье мы познакомим вас с основами дзета-функции Римана, её значением, применением и возможностями для её вычисления с помощью онлайн-калькулятора. Использование калькулятора значительно облегчает вычисления и помогает исследователям и студентам быстро получать точные результаты при работе с этой сложной функцией.
Дзета-функция Римана, обычно обозначаемая как ζ(s), представляет собой комплексную функцию, определённую для комплексных значений переменной sss. Функция была впервые введена немецким математиком Бернхардом Риманом в 1859 году в его знаменитой работе о распределении простых чисел. В её классическом виде, для s>1, дзета-функция Римана определяется как бесконечный ряд:
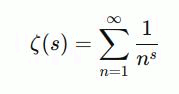
Здесь n — это целое число, а s — комплексное число, причём действительная часть s должна быть больше 1, чтобы ряд сходился.
Основные свойства дзета-функции Римана
-
Аналитическое продолжение. Хотя ряд для дзета-функции сходится только при Re(s)>1, существует способ аналитического продолжения этой функции на всю комплексную плоскость, за исключением точки s=1. Это продолжение позволяет вычислять значения функции и в тех областях, где ряд не сходится. Для этого используется функциональное уравнение и другие методы теории аналитических функций.
-
Функциональное уравнение: одной из особенностей дзета-функции является её функциональное уравнение. Оно связывает значения функции в точках s и 1−s, что играет важную роль в теории распределения простых чисел. Это уравнение имеет вид:
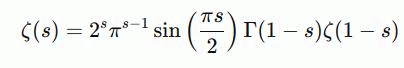
где Γ(s) — гамма-функция, которая является расширением факториала для комплексных чисел.
- Нули дзета-функции Римана: одним из самых интересных аспектов дзета-функции Римана является её нули. Если рассматривать значения функции, при которых она становится равной нулю, то для комплексных чисел sss существует бесконечное множество таких точек. Самыми важными из них являются так называемые неявные нули дзета-функции, которые находятся на критической прямой с действительной частью Re(s)=1/2. Все они лежат на критической прямой, если гипотеза Римана верна. Это важное утверждение, которое до сих пор не доказано и является одной из самых известных гипотез в математике.
Гипотеза Римана, выдвинутая самим Риманом, утверждает, что все неявные нули дзета-функции имеют действительную часть равную 12\frac{1}{2}21. Это одно из важнейших предположений в теории чисел, и его доказательство или опровержение станет значительным прорывом в математике. Применение гипотезы Римана к теории простых чисел приводит к улучшению понимания их распределения. Если гипотеза окажется верной, то это даст новые способы оценки распределения простых чисел в больших интервалах.
Гипотеза Римана остаётся неразрешённой проблемой, но при этом она имеет важное значение в различных областях науки, таких как криптография, математическая физика и теория чисел.
Дзета-функция Римана не только имеет важное теоретическое значение, но и находит применение в различных областях науки. Одним из главных направлений является её связь с распределением простых чисел. Простые числа — это такие числа, которые делятся только на 1 и на себя, и они играют фундаментальную роль в теории чисел. Риман, изучая дзета-функцию, связал её с простыми числами через формулу Эйлера:
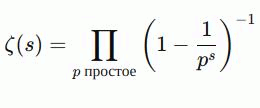
Это выражение позволяет изучать простые числа через поведение функции, что помогает в анализе их распределения. Чем лучше мы понимаем поведение дзета-функции, тем точнее можем оценить, как часто простые числа встречаются в разных интервалах.
Дзета-функция Римана также нашла практическое применение в криптографии. Простые числа играют ключевую роль в многих алгоритмах шифрования, таких как RSA, где используются большие простые числа для создания публичных и приватных ключей. Понимание распределения простых чисел и их свойств помогает в создании более надёжных и безопасных криптографических схем.
Дзета-функция Римана — это не только центральный объект теории чисел, но и важный инструмент для изучения фундаментальных аспектов математики, таких как распределение простых чисел. Гипотеза Римана, связанная с ней, продолжает оставаться одной из самых значимых нерешённых проблем в математике, и её доказательство или опровержение окажет глубокое влияние на всю математическую науку. Важность этой функции простирается за пределы теории чисел и находит своё применение в таких областях, как криптография и математическая физика.
